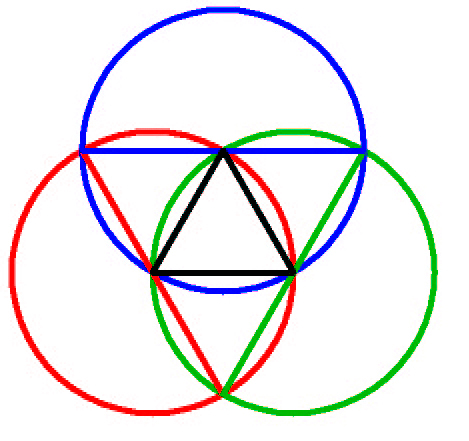
GEODESIC PROPERTIESThe Geodesic Dome is inherently stable due to it's Geodesic -Triangulated network of members. It encloses a greater volume of space with less material than most other of structures. It is readily Mass-Producible, Modularly Expandable, Readily Transportable and Quickly Erectable. Geodesic Domes offer High Strength Relatively Low Cost, Quick Erecting, Clear Span Structures.
Performance
A good index to the performance of any building is the structural weight required to shelter a square foot of floor (from the weather). In a conventional building, it is often 50 lbs per sq. ft.
By constructing a frame
of generally spherical form,
in which main structural elements
are interconnected
in a geodesic pattern
of approximately great circle arcs
intersecting to form a three-way grid
and then covering (lining) this frame work
with a film or fabric skin ....
a wt./ft of approx. 0.78 lbs/sq. ft
can be achieved.
Geodesic spherical structures
being framed entirely
of great circle chords,
and inherently omni-triangulated,
give the strongest structure
per weight of material employed.
The higher the frequency,
the more ephemeral the tensegrity complex
and the less the total weight of the structure
per given level of performance
The whole structure
is also less vulnerable
to the total violations
of any or many
inwardly or outwardly originating
impinging forces.
Load Distribution
The three-way grid of structural members in a geodesic dome results in substantially uniform stressing of all members.
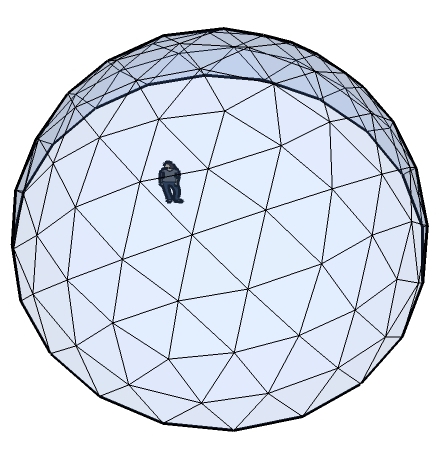The framework itself
acts almost as a membrane
in absorbing and distributing loads.
If the structural members are aligned
with the lines of geodesic grids
then the resulting framework
will be characterized
by more uniform stressing
of the individual members
than is possible
with any construction heretofore known.
In geodesic tensegrities,
all tension members cross one another
in great circle chorded triangulations,
thus providing
the highest possible dimensional stability.
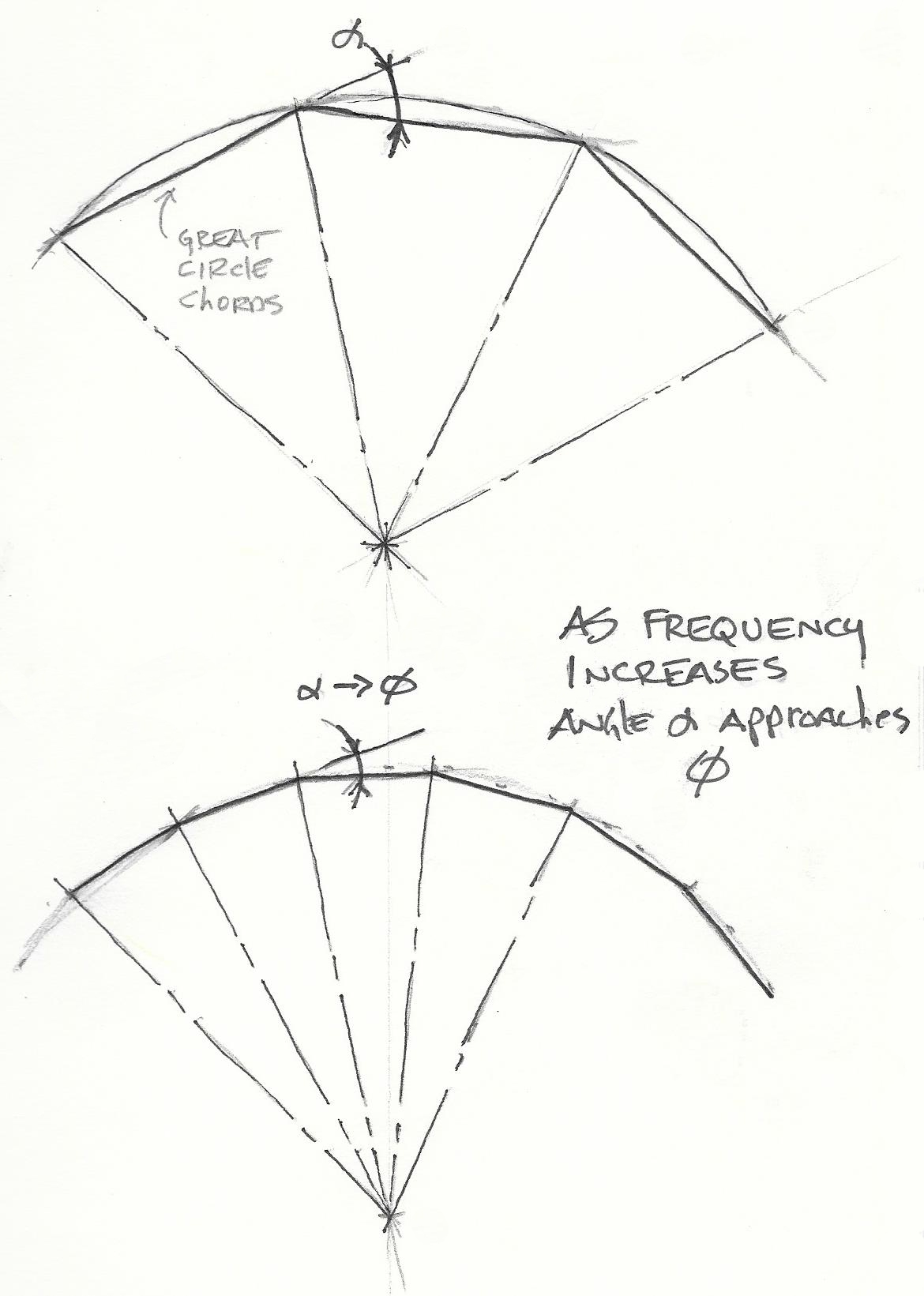
Great circle arcs
represent the limit
of structural transformative tendency
of outward surface tensing
by internal pressure.
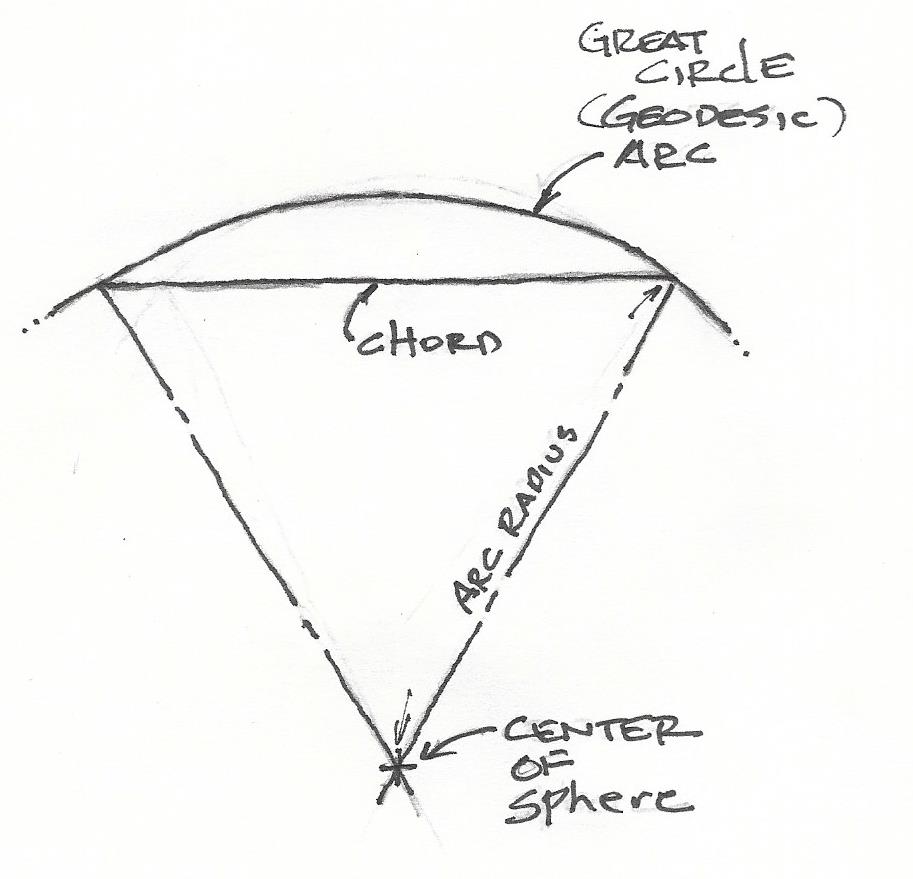Great circle segment chords
represent the limit structural optimum
for axis of compression-resisting columns
opposing external pressure
by surface spreading.
As vertices and trussed faces multiply
at a given diameter,
there are greater numbers
of shorter compression columns
to share the load -
to be realized progressively
with more economical slenderness ratios.
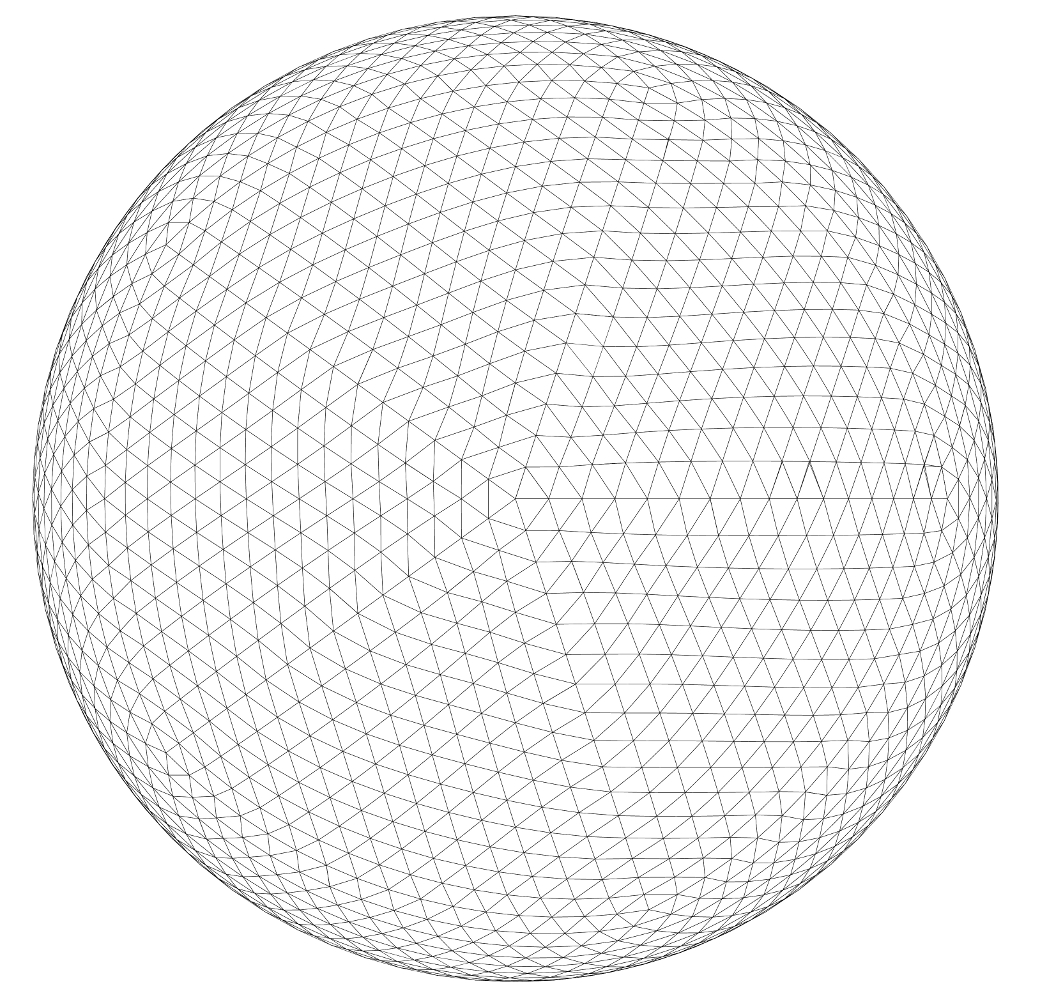An increased number of vertices and edges
provide more and dispersed structural interactions
for resisting concentrated loads
from more directions.
If a further approach to the congruence
of all-trussed chordal polyhedra
with arc-structured spheres
can be accomplished,
not only
will the vertices and trussed facets (penetration points) multiply,
it provides increased advantage
in more directions
against concentrated loads
and more directions of penetration.
As the number of trussed facets increase,
the convex vertexial interactions
approach a zero attitude condition,
which,
though ideal for tension or internal pressure,
tends to allow
concentrated external loads
to push the convex chordal vertices inside-out
(i.e. to a dimpled or concave condition).
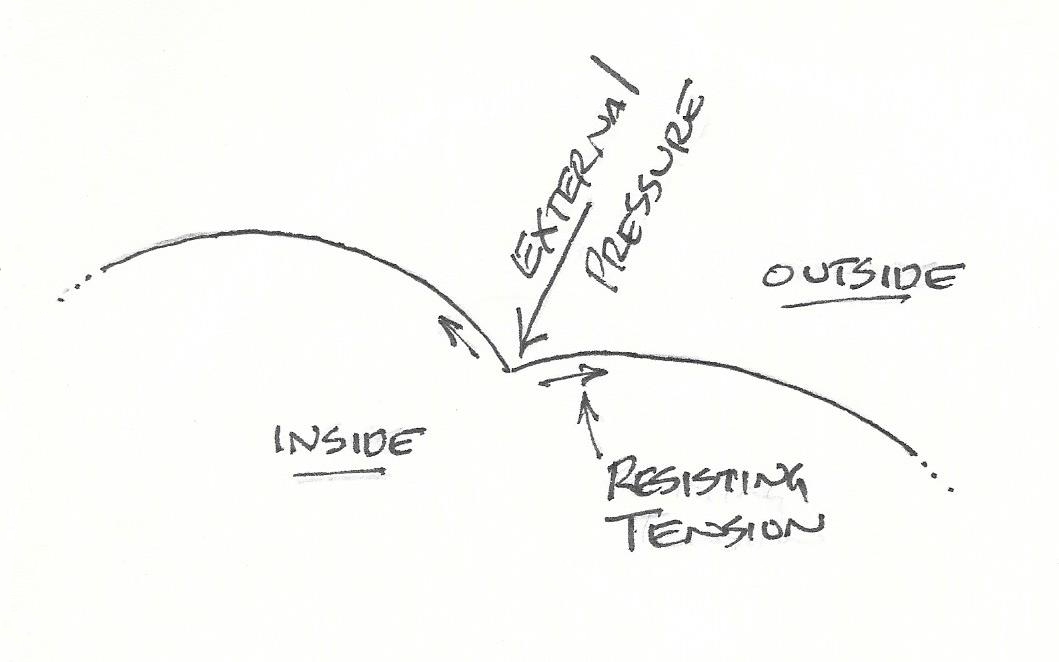
In the dimpled or concave condition,
continuing concentrated external pressure
will be resisted
by a tension increase
in omni-surface direction
(eg. as a rubber ball
draws on its skin
as it resists punching in
& gains reaction
& springs back
causing bounce).
This behavior was dramatically demonstrated to me
when I climbed a 4 Frequency, 16 ft Radius dome
constructed of 1/2" electrical metal conduit (emt).
This material is not strong enough
to support my weight (~240 lb)
in the middle of a 4 foot long strut,
though the Dome Vertices easily support me
and show no deflection,
when loaded with my weight.
So, I had climbed to the 3rd level from the ground
and was beginning to retreat,
when I stepped into the middle of a strut with great force,
severely bending the strut.
This initiated a failure
by pulling a vertex
in toward the center of the dome.
and I began to sink,
as several other vertices
were pulled inward.
However,
This failure stopped
and I was buoyed up
by the surrounding unsunken dome
as though in a net .
and from here I slunk to the ground.... :-)
AMEN to that, Thank God & Bucky.
Tensegrity
The word Tensegrity is a contraction of the phase "TENSional intEGRITY". The word integrity points to structural completeness. In a tensegrity, the continuity is in the tensional network which is a sort of stressed cage in which compressions float.
The great structural systems of the universe
are accomplished
by island-ed compression
and omni-continuous
tension.
All Geodesic Domes
are tensegrity structures
whether or not
the tension/island-ed compression differentiations
are visible
to the observer.
Geodesic domes
are designed
as enclosing tensile structures
to meet discretely, ergo non-redundantly,
the patterns of outward forces.
In the geodesic tensegrity sphere,
each of the entirely independent
compressional chord struts
represent
2 oppositely directioned,
force paired molecules.
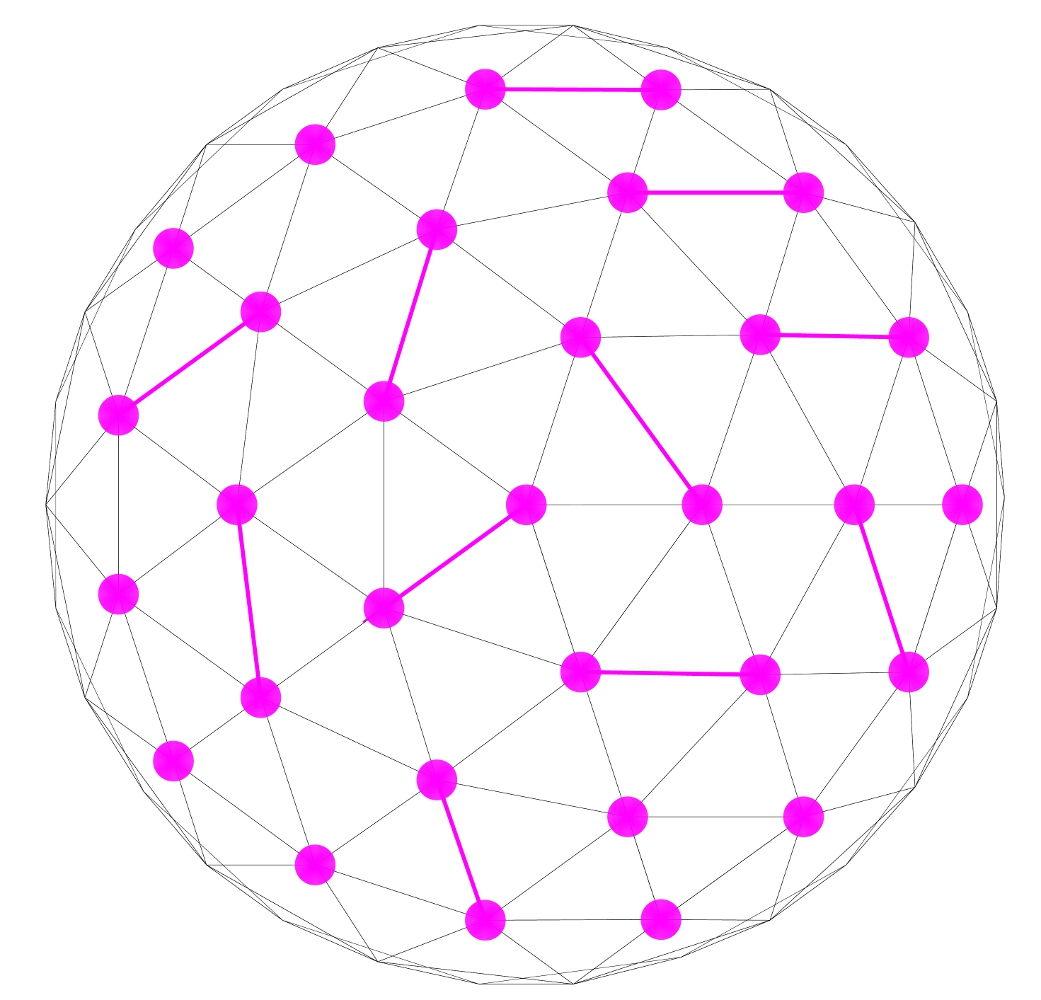The tensegrity compressional chords
do not touch one another.
They operate independently,
each trying to escape
outwardly from the sphere.
These tensegrity compressional chords
are restrained
by the spherical tensional integrities
closed network of connectors
which alone can complete the great circle paths
between the ends
of the entirely separate,
non-directly interconnecting
compressional chords.
The tension lines clearly show
that the struts each pull away
from each other (nearest neighbor)
and strain to escape radially
outward of the system.
Were the chordal struts
to be pushing circumferentially from the sphere
their ends would touch one another
or slide by one another.
The paired-outward caroming of the 2 chord ends
produces
a single,radially outward force
of each chord strut.
BTW:
Bucky filed and recieved a patent related to this concept.
Tensile Integrity Structures -U.S. Patent #3,063,521
Expansion / Contraction
An impressive behavioral characteristic of tensegrity spheres, witnessed at low frequencies, is that when any two islanded struts 180 degrees apart around the sphere are pulled outward from one another the whole sphere expands symmetrically. When the same two struts are pushed toward one another the whole sphere contracts symmetrically.
When the polar pushing together or pulling apart ceases
the tensegrity sphere assumes a radius
halfway between the radii
of the most pullingly expandable
and pushingly contractible conditions
(i.e. it will rest in dynamic equilibrium).
The equilibrium state
which tensegrity spheres spontaneously assume
is the state wherein all parts are most "comfortable"
but are always subject to spherical oscillability.
Comfort here implying that the system
has no external or internal forces applied
other than the forces of the gravitational fields
in which it exists.
The tightening
of any one tension member
or increasing the length of any one strut
tightens the whole system uniformly
as is tunably demonstrable.
Next
Table of Contents