Domes have not been widely used partly because they are mathematically derived structures & the mathematics haven't been easily available. Though the derivation is tedious, the resultant basic pattern allows rapid simple calculation of strut lengths. What we need to know structurally is the length of the chordal lines between any 2 adjacent points in the 3 way great circle grid (& in some cases the angles @ which they intersect ) . The distance between these points are the strut lengths. Allowances should be made for the fastening system. The lengths of the struts are substantially equal but not precisely so. The slight differences in the lengths of different struts in a given framework determine the radius of the dome. The slight differences between the lengths of the individual struts in turn create slight differences between the angles of the substantially equilateral triangles & this results in a spherical grid structure in which all main structural members are in geodesic alignment or are chords of great circles of a common sphere. The number of different strut lengths in any given framework based on a spherical icosahedron varies in accordance with the frequency of the great circle grids. At an edge frequency of 16, the arc & chord tend to "indistinguishable" differences of dimension. There need never be any greater complication as to the number of struts than is represented by frequency 16. With frequency 16, all conditions of framework design are satisfied with 56(?) different strut lengths (the same framework of frequency 8 can be constructed of 16 different lengths & with frequency 4 only 5 different strut lengths are required). The higher the frequency of the system the lesser in dimension will the arc, chord & arc altitude increments become. The arc, chord & arc altitude dimensions co-vary @ identical rates & therefore are uniformly proportional for any given frequency. In the pattern of the geodesic tensegrity sphere, the number of hexagons, triangles & chords may be multiplied in regular arithmetical or geometric series. In the pattern of the geodesic tensegrity sphere, 12 & only 12 pentagons will persist as constants, as will the number of triangles occur in multiples of 20's & the edges in multiples of 6. The strut lengths are determinable mathematically or graphically.
GRAPHICAL PROCEDURE
One method of determining strut lengths is to construct a paperboard hemisphere to a convenient scale & layout vertices of one of the faces of a spherical icosahedron on its surface. These vertices are then connected by drawing great circle lines (spherical straight lines) there between. The edges of the triangle defined by these lines are next divided equally into the number of units represented by the selected grid frequency. The division points are then connected by drawing great circle lines to the points along one edge are connected to every second point on another edge. This yields a completed 3-way grid pattern. The length of the chordal struts is measured directly with the use of ordinary draftsmans dividers - allowances being made for strut fastenings.
MATHEMATICAL PROCEDURE ( for Strut Length Calculation )
Spherical Geometry: Most of the problems of geodesic mathematics can be solved with the aid of the Spherical Coordinate System ( Spherical Trigonometry ). A unique point is specified by a distance (radius) & 2 angles.
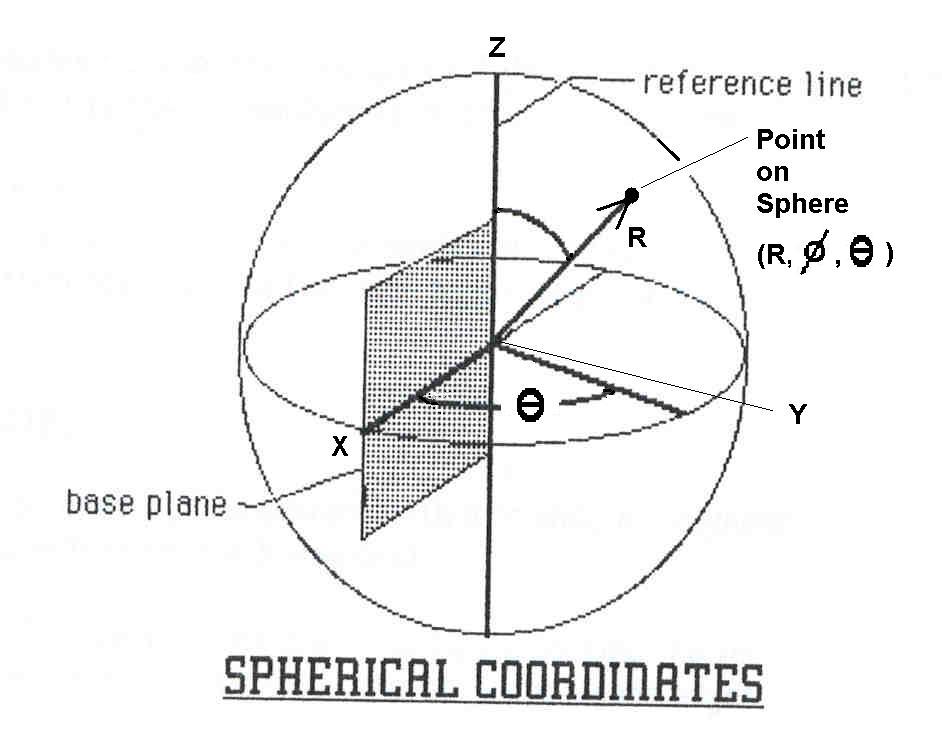A spherical coordinate has the format (R,θ,ø).
R is the distance from the point of intersection
to the point to be designated.
Given a line of reference & a base plane through the line of reference
Theta (θ) is the angle measured perpendicular with respect to the base plane
(or "X" axis).
Phi (ø) is the angle with respect to the line of reference (or "Z" axis).
If the coordinates of the 2 points are known,
the chordal distance between them is :
D = √ (R12 + R22 - 2R1R2(cos θ1cos θ2 + cos (ø1-ø2) sin θ1sin θ2))
in the spherical case R1 = R2 = 1.
If the points described are on the surface of a sphere,
R can be designated as 1 (unity) & virtually disregarded.
If the envelope of the system is other than spherical,
the varying values of R must be taken into account.
Every point on a great circle arc
is @ full radius distance from the spheres center.
The chord & 2 radii form an isosceles triangle.
The distance between the mid-arc & mid-chord is called the arc altitude.
In the icosahedron,
each great circle arc edge has a central angle
of 63 deg. 26 min. 06 sec. (1.1071 radians)
For an octahedron, the central angle is 90 Deg.
The tetrahedron has as a central angle of 109.10 Deg.
In a geodesic dome, the triangles involved are not equilateral
(but are very close) -
it is their departure from equilaterality that provides curvature.
Given a single vertex,
if we consider the sum of the angles around it,
the difference between this sum & 360 degrees (flatness)
is called spherical excess.
The Grid
All break down systems start with a triangular polyhedral face & subdivide it with a 3 way grid. Triangular subdivisions are made by connecting the face divisions with lines parallel with the the edges of the polygons edges. The number of modules into which each edge of the spherical icosahedron (or octahedron or tetrahedron) is divided is largely a matter of choise. The number of modules is called the frequency (of the structure). The arc edge subdivision number is termed the frequency of the system. In developing the triangular subgridding of the icosahedral geodesic prime structural system, the great circle arc edges of the icosahedron are equally subdivided into 2, 3, 4 or more equal arc increments. The number of arc increments is dependant on engineering calculations considering variables such as diameter of the structure, structural properties of the construction materials, logistics of delivery, installation & assembly. All the calculations required for the design of geodesic domes may be derived from the 3 basic triangles of the 3 basic structural systems (the 120 right triangles of the icosahedron, the 48 rt. triangles of the octahedron & the 24 rt. triangles of the tetrahedron). All the great circle behaviors occurring around the whole sphere take place within just 1 of those 3 basic right triangles & repeat themselves in all others. The data mathematically developed with in the 3 basic triangles become constants for spheres of any size. See Facet Diagrams in Appendix. A break down system provides the criteria for choosing a polyhedra. The vertices of the given grid are pushed out till they are a common distance from the center(for spheres) or a harmoniously varying distance for other contours (eg ellipses). CLASS 1 (alternative) break down system - grid lines run roughly parallel to the edges of the polyhedron face. There are a number of different techniques to specify vertices, each yielding slightly different strut lengths. METHOD 1 - θ coordinates are spaced equally down the edges of the face of the given polygon (eg 30, 60, 90 degrees). This is the method used in this study. Method 1 yields triangles varying less in size & more in shape. METHOD 2 - taking the triangular polygon face, the edges are equally divided then the division points are projected outward from dome center @ equal radius. Sub-triangles are made as before. Next Table of Contents