Drawing a Grid Diagram
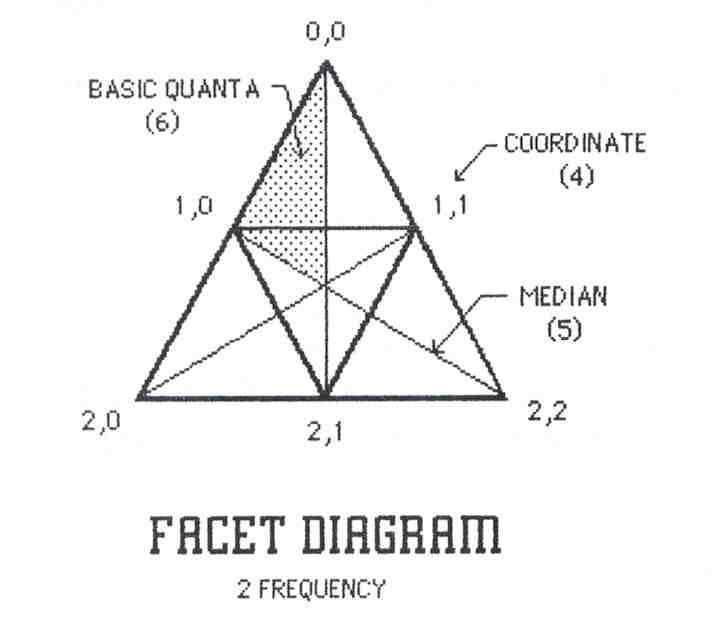 (1) Sketch an equilateral triangle.
(2) Subdivide the edges into N parts for N frequency.
(3) Join the points of subdivision with a 3 way grid.
(4) Start @ the top vertex & number all the crossing points for the frequency N
(the 1st point will be 0,0 & the last point will be N,N )
every point has a 2 number designation. (See diagram)
(5) Draw the 3 medians of the face triangle.
(6) The medians describe 6 right triangles,
each containing the whole symmetry system of the polygon.
This pattern is the basic quanta of this system.
The structure consists of repetition of this.
(7) If the structure considered is spherical,
chord factors are needed only for the break down edges
that lie partly or completely within the symmetry triangle.
(8) For a sphere,
the only coordinates required are the end points of the edges
contained by the symmetry triangles.
(9) The system repeats symmetrically.
(10) If the top left symmetry triangle is used
the numbers to be manipulated are handier as many values are 0.
(1) Sketch an equilateral triangle.
(2) Subdivide the edges into N parts for N frequency.
(3) Join the points of subdivision with a 3 way grid.
(4) Start @ the top vertex & number all the crossing points for the frequency N
(the 1st point will be 0,0 & the last point will be N,N )
every point has a 2 number designation. (See diagram)
(5) Draw the 3 medians of the face triangle.
(6) The medians describe 6 right triangles,
each containing the whole symmetry system of the polygon.
This pattern is the basic quanta of this system.
The structure consists of repetition of this.
(7) If the structure considered is spherical,
chord factors are needed only for the break down edges
that lie partly or completely within the symmetry triangle.
(8) For a sphere,
the only coordinates required are the end points of the edges
contained by the symmetry triangles.
(9) The system repeats symmetrically.
(10) If the top left symmetry triangle is used
the numbers to be manipulated are handier as many values are 0.
THE GEODESIC ALGORITHM EXPLAINED
The geodesic algorithm is the mathematical procedure for finding the strut lengths of a geodesic dome. This algorithm utilizes spherical trigonometry to solve for spherical coordinates of the vertex points of a facet diagram for a given frequency & radius dome. Then the chordal distances between adjacent vertices are computed using the spherical coordinate distance formula. These distances are the strut lengths. Solving for the vertex coordinates involves solving a series of 4 spherical triangles. See Diagrams 1 - 4 .
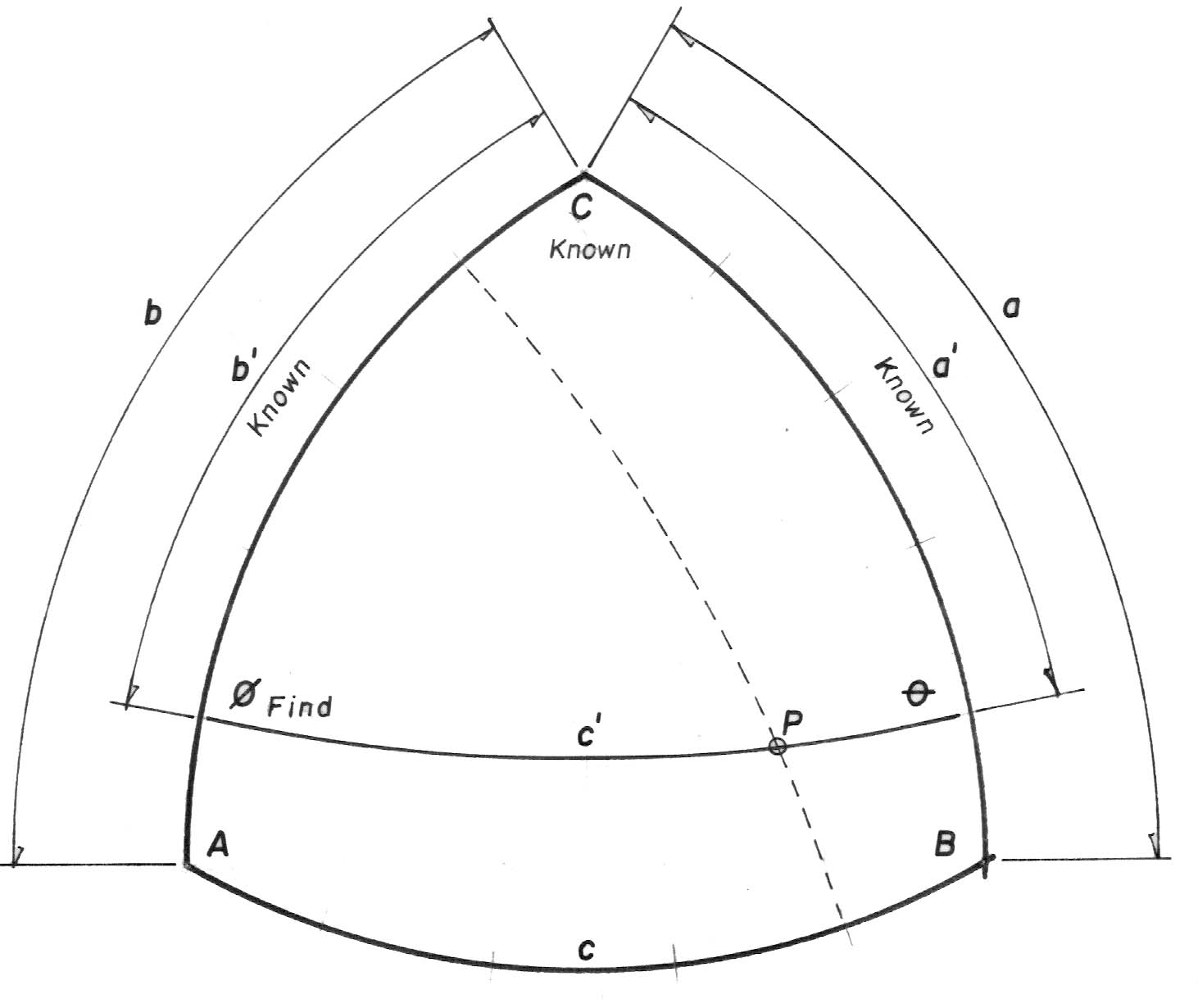 Diagram 1: We begin with a spherical icosahedral facet (spherical triangular side)
with dimensions of 72 degrees @ each vertex angle (A, B & C)
& sides (a, b & c) of 63 degrees, 26 minutes & 06 sec.
(Note: in spherical trig, sides are dimensioned in terms of angles with respect to dome center.)
With a frequency of F, the sides are divided into F parts;
so that Sides b' & a' are known ( selected so that the vertex to be calculated is intersected )
as well as Angle C.
Using spherical trig equations 1, 2 & 3 ,
Angle ø is found for use in Solution 2.
These 3 equations & equation 4 embody the Side-Angle-Side (SAS) Subroutine.
See the end of this chapter for these equations.
Diagram 1: We begin with a spherical icosahedral facet (spherical triangular side)
with dimensions of 72 degrees @ each vertex angle (A, B & C)
& sides (a, b & c) of 63 degrees, 26 minutes & 06 sec.
(Note: in spherical trig, sides are dimensioned in terms of angles with respect to dome center.)
With a frequency of F, the sides are divided into F parts;
so that Sides b' & a' are known ( selected so that the vertex to be calculated is intersected )
as well as Angle C.
Using spherical trig equations 1, 2 & 3 ,
Angle ø is found for use in Solution 2.
These 3 equations & equation 4 embody the Side-Angle-Side (SAS) Subroutine.
See the end of this chapter for these equations.
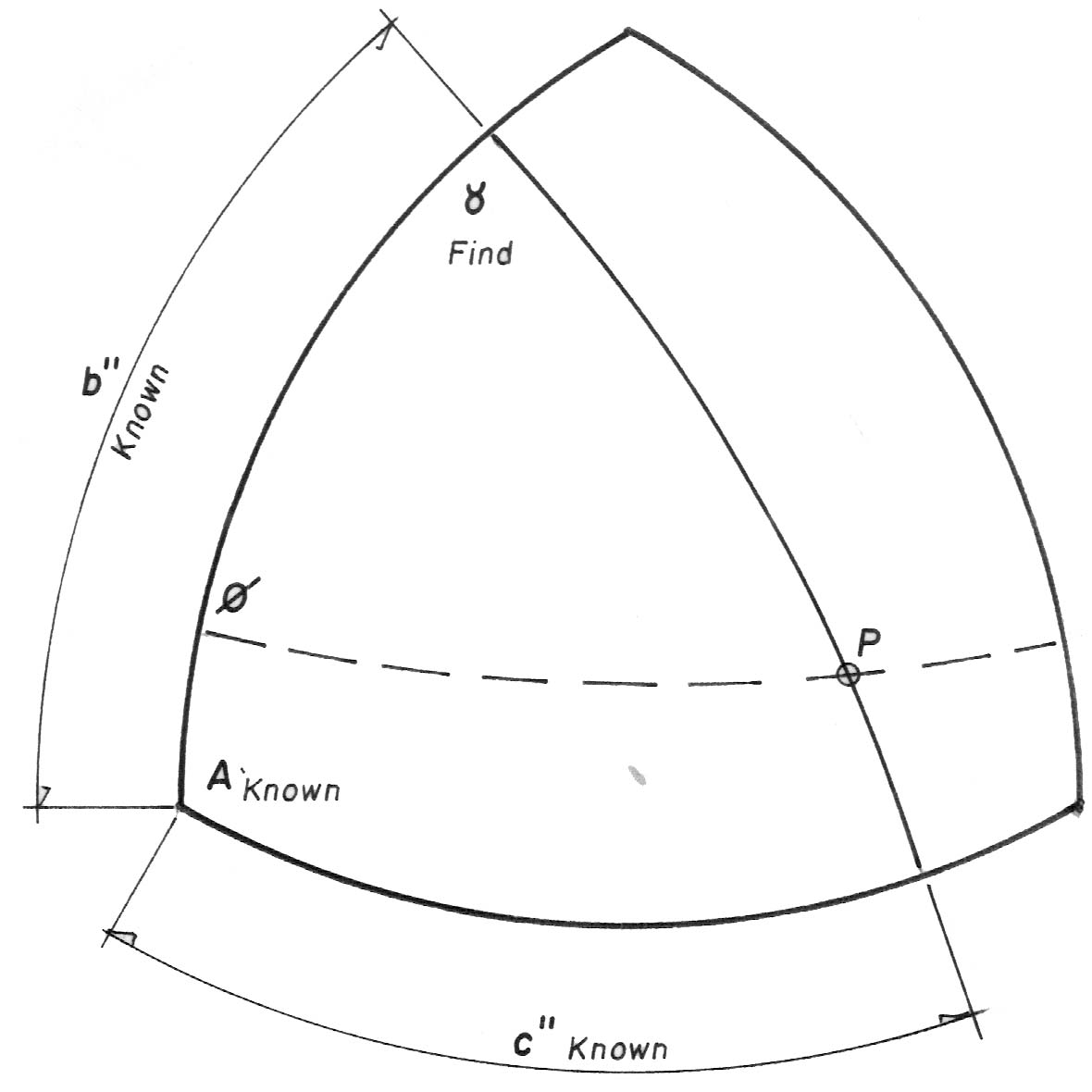 Diagram 2: Angle A is known to be 72 Degrees & b'' & c'' are known
( selected so that the vertex to be calculated is intersected ).
Angle γ is to be found,
so again equations 1, 2 & 3 (the SAS Subroutine) are used to solve for γ.
Both angles ø and γ are used in Diagram 3 (Solution 3).
Diagram 2: Angle A is known to be 72 Degrees & b'' & c'' are known
( selected so that the vertex to be calculated is intersected ).
Angle γ is to be found,
so again equations 1, 2 & 3 (the SAS Subroutine) are used to solve for γ.
Both angles ø and γ are used in Diagram 3 (Solution 3).
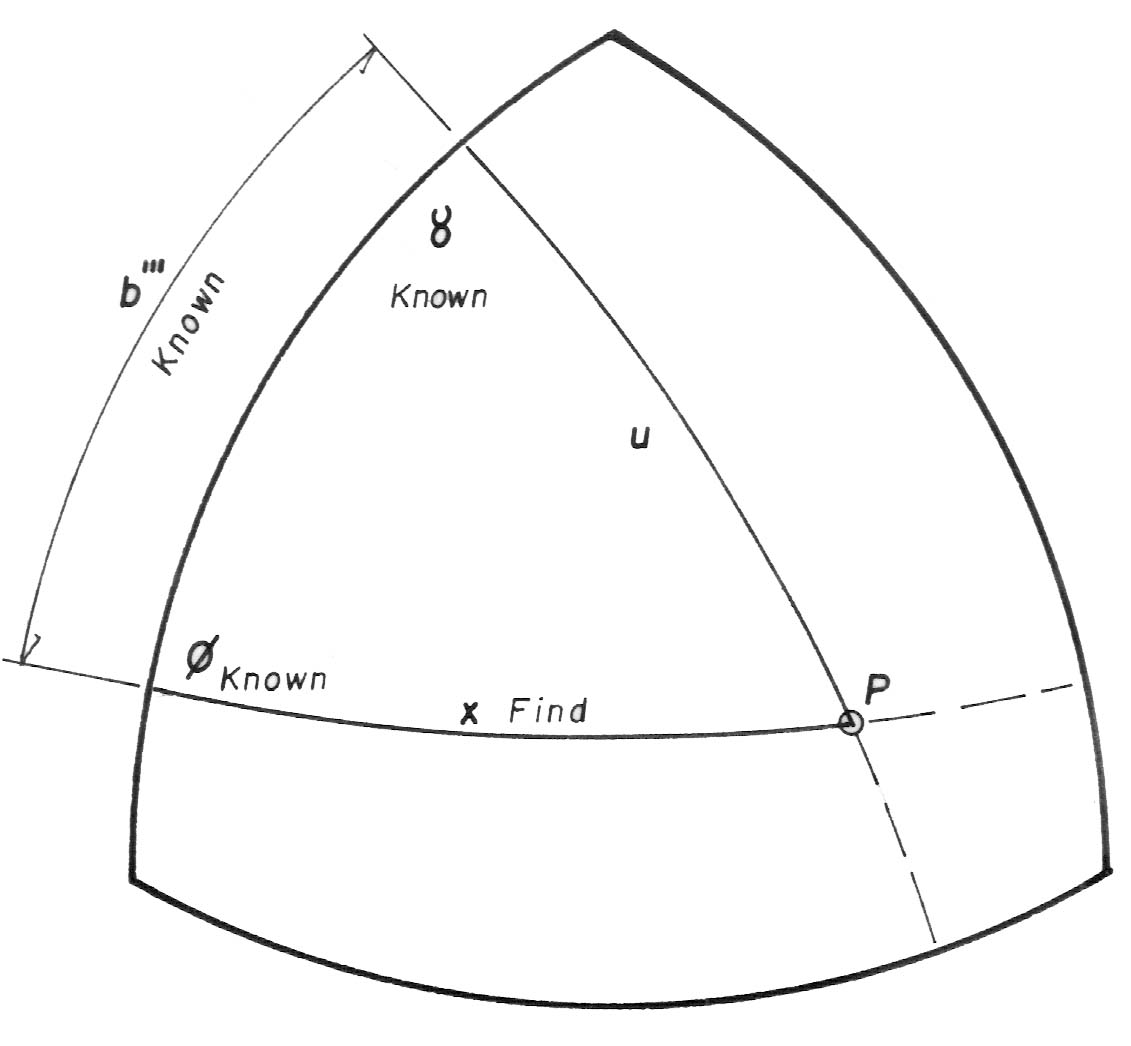 Diagram 3: Using Angles ø and γ and the difference between Sides b' & b'' (= Side b''')
we solve for X.
This time, equations 5, 6 & 7 ( the Angle-Side-Angle (ASA) Subroutine)
are used to obtain Side X.
Diagram 3: Using Angles ø and γ and the difference between Sides b' & b'' (= Side b''')
we solve for X.
This time, equations 5, 6 & 7 ( the Angle-Side-Angle (ASA) Subroutine)
are used to obtain Side X.
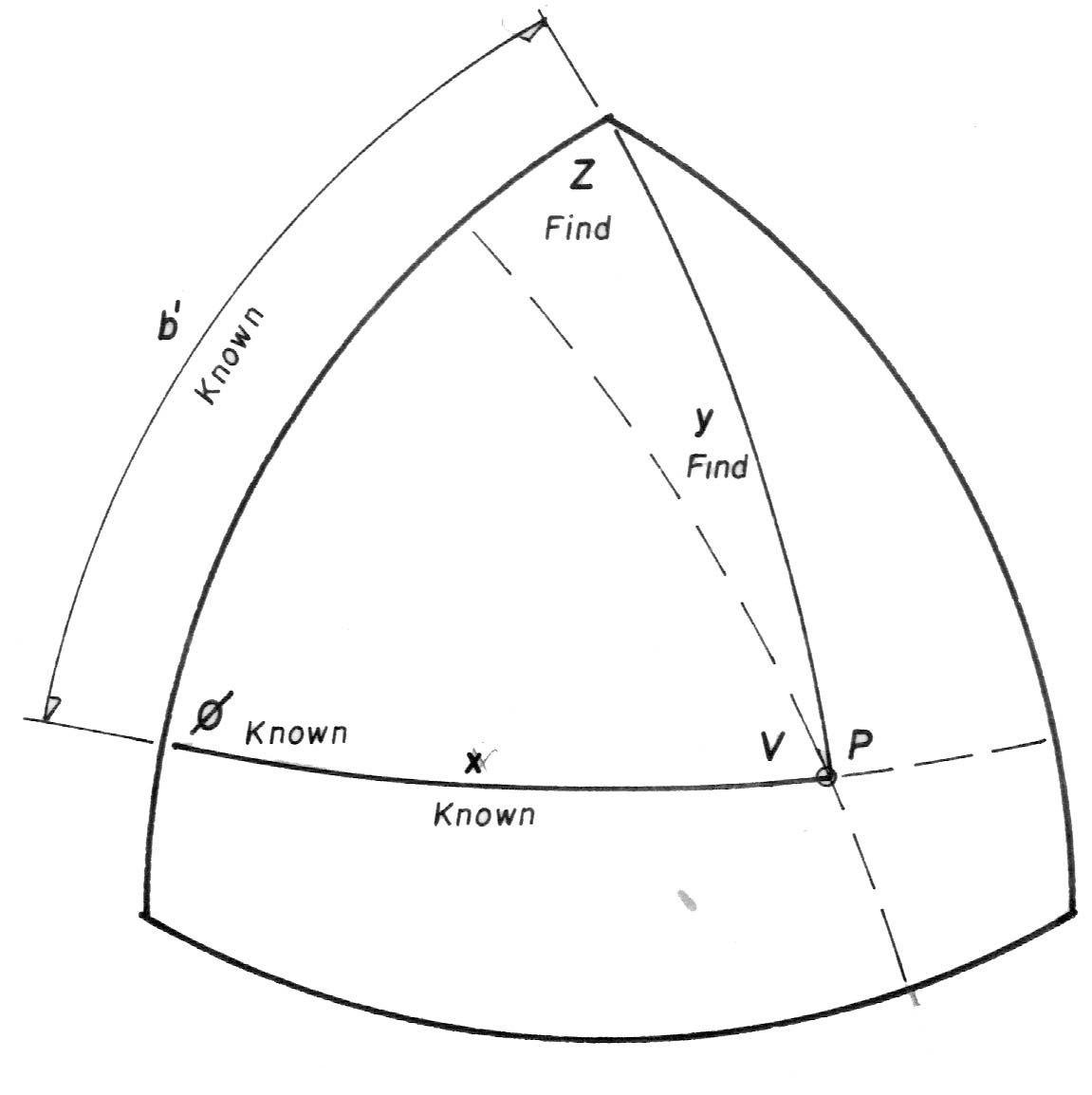 Diagram 4: This is the final step in obtaining the spherical coordinates for a given vertex.
We now have Side b', Side X and Angle ø from which we can obtain Angle Z
(using Eq. 1, 2 & 3) & Side Y (using Eq. 4 ) being the coordinates of point P.
The coordinates for each adjacent vertex are applied to Equation 8
to obtain the strut lengths
which are the chordal distances between the vertices.
Diagram 4: This is the final step in obtaining the spherical coordinates for a given vertex.
We now have Side b', Side X and Angle ø from which we can obtain Angle Z
(using Eq. 1, 2 & 3) & Side Y (using Eq. 4 ) being the coordinates of point P.
The coordinates for each adjacent vertex are applied to Equation 8
to obtain the strut lengths
which are the chordal distances between the vertices.
SPHERICAL TRIG EQUATIONS & NOTES
Note: In spherical trig, both angles & sides are measured angularly. SAS With equations 1, 2 & 3 an angle (ø) can be found given 2 sides (A & B) & the included angle β (1) ø + δ = 2 arctan ([cos1/2(a-b) / cos1/2(a+b)] cot β) (2) ø - δ = 2 arctan ([sin1/2(a-b) / sin1/2(a+b)] cot β) (3) ø = [(ø+δ)+(ø-δ)]/2 the third side (C) is solved for using eq. 4 after solving eq. 1, 2 & 3 (4) c = 2 arctan ([sin 1/2(ø+δ) / sin 1/2(ø-δ)] tan 1/2(a-b) ) (where ø, δ β are angles ; a, b & c are sides) ASA With Equations 5, 6 & 7 a side (a) can be found given 2 angles (ø & δ) & the included side (c) (5) a + b = 2 arctan ([cos1/2(ø-δ) / cos1/2(ø+δ)] tan 1/2c) (6) a - b = 2 arctan ([sin 1/2(ø-δ) / sin1/2(ø+δ)] tan 1/2c) (7) a = [(a+b)+(a-b)]/2 (where a,b & c are sides ; ø & δ are angles) Utilizing the first 7 equations, the polar coordinates of each point on a grid can be derived. These coordinates can then be plugged into the Chordal Distance Formula (Equation #8) yielding the strut (chord) length between 2 points on a sphere. (8) D = √[r(1)**2 + r(2)**2 - 2*r(1)*r(2)*(cos(δ(1))*cos(δ(2)) + cos (ø(1)-ø(2)) * sin δ(1) * sin δ(2)] in the spherical case r(1) = r(2) = 1. See diagram for variables.
CHORD FACTORS / BASE RATIO
After the strut lengths have been found, the repetitive pattern within the facet is established by graphical construction of the medians of the facet (see GEODESEMETRY Section ) & numerical balancing of strut length distribution to obtain overall symmetry within the facet while maintaining the major arc lengths. Balancing is actually averaging; for each strut position in the symmetry triangle take the average of all strut lengths in the facet at that particular locus. The resulting "balanced" strut lengths are then reduced to the most general form called the BASE RATIO (Chord Factor) by dividing the strut lengths by the icosa-edge strut length. This yields a value of 1 for icosa struts & a slightly higher value for the others. This base ratio is easily remembered & is used for any radius dome of the particular frequency. See the facet diagrams in the appendix. After the base ratios have been derived, further use of the geodesemetry algorithm is unnecessary and even ill advised because it is not symmetrical (also much slower ). There is a set of unique Base Ratios (also called Chord Factors) for each frequency, regardless of radius. See the Appendix for Facet Diagrams for Base Ratios for each frequency 2 thru 16. Uniform dimensions, chord factors & ratios may be listed for any size dome. The only numerical variable in geodesic spherical structures is that of the systems radius. The name chord factor is assigned to all the constant lengths of a spheres connecting lines whether between any 2 spherical surface lengths or between 2 concentric spheres that are inter-triangularly trussed (or related structuring, i.e. door openings). The spherical surface angles of the sphere & the central angles may be expressed in the same decimal fractions - which remain constant for any size sphere since they are fractions of a unit finite whole system. Central angles of great circles are defined by 2 radii, the outer ends of which are connected by both an arc and a chord- which arc and chord are directly proportional to each unique such central angle. The chord and the 2 radii form an isosceles triangle. The distance between the mid-arc and the mid-chord is called the arc altitude. The frequency of modular subdivision of the edge of the icosahedrons facets may be multiplied @ will once the spherical trigonometry rates of change of central & surface angle subdivisions have been solved. This is the essence of geodesic structures.
PRACTICAL USE OF BASE RATIO
Now that you have the Base Ratios (Chord Factors), how do you put them to practical use ? You need to define the parameters of the dome. What Radius do you want/need ? What size of members is acceptible ? What Frequency ? Which of these factors are most important to you ? For instance, If you need a given radius, to determine the resulting strut length you need to pick a frequency. Then the short answer is S = 2(R(SIN((1.1071/F)/2))) Where: S = Strut Length R = Radius (B20) F = Frequency (B19) and the angle in this case is expressed in radians. For Excel cut and paste : =2*(B20*(SIN((1.1071/B19)/2))) (B20 and B19 are arbitrary spreadsheet cells, holding the values of Radius and Frequency) By varing the radius and the frequency, you change the strut size, allowing you to arrive at your optimal size strut for a given application. Below is a sketch of the derivation of that formula.
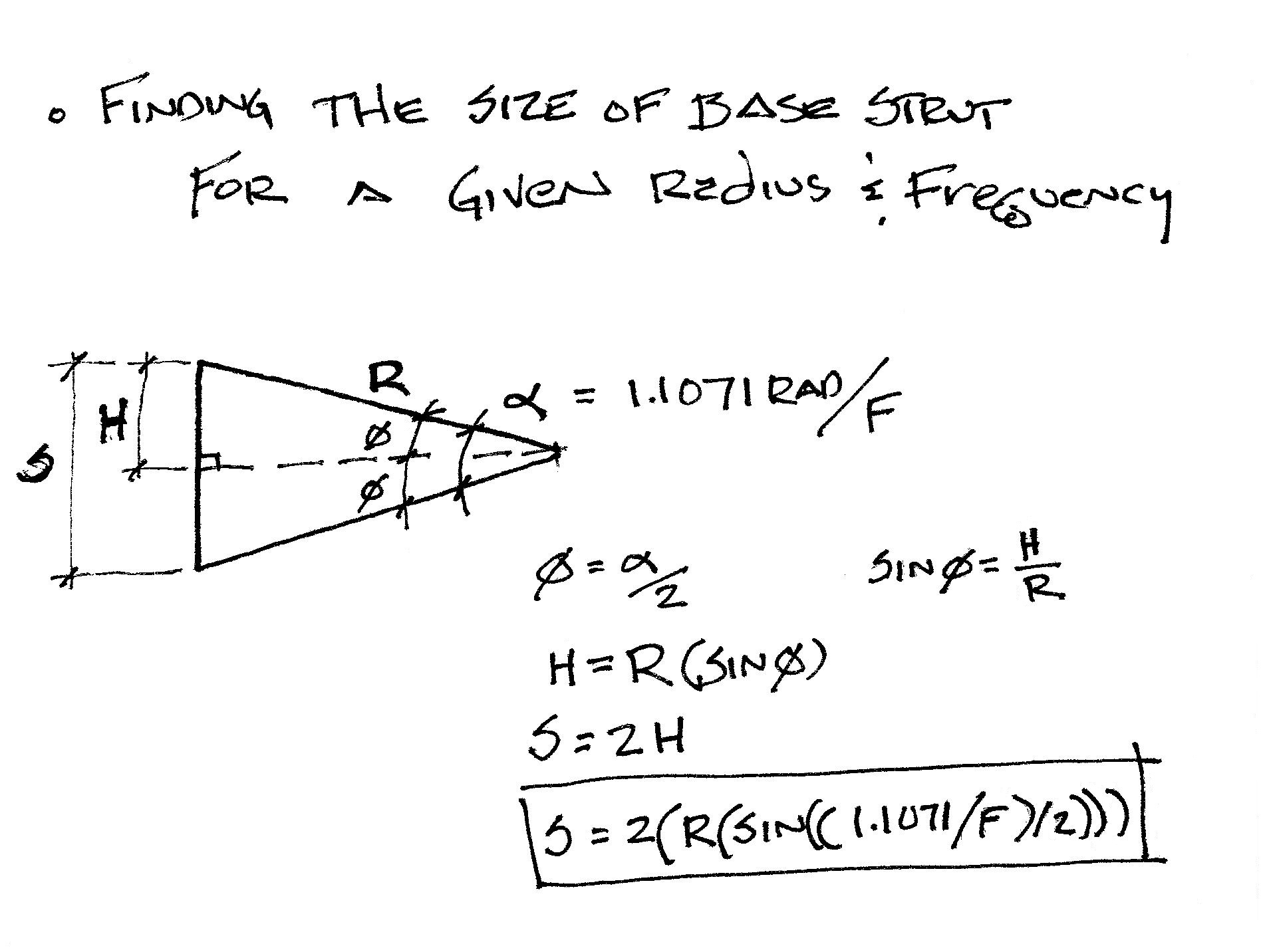 This Strut Length , S , is for the iscosa edge struts
which are the struts of length 1 in the facet diagrams.
To obtain the lengths of the other struts
multiply "S" by their chord factors.
This Strut Length , S , is for the iscosa edge struts
which are the struts of length 1 in the facet diagrams.
To obtain the lengths of the other struts
multiply "S" by their chord factors.
DOME SERIES
In order to facilitate interchangability of struts between domes, domes of consecutive frequencies can be based on a standard icosa-edge size. This is to say that within a series, icosa-edge struts stay the same and dome size changes are made by changing frequency. For a given series, the radius divided by the frequency is constant (i.e. series number = radius/frequency or series x freq. = rad. ). For example, consider the #4 Series with a 4.43 Icosaedge strut: 4 x 2 freq. = 8' rad. , 4 x 3 freq. = 12' rad. , 4 x 4 freq. = 16' rad. , etc. Building domes of a given series makes for interchangable parts while disregarding or switching series means more & different strut sizes. Next Table of Contents