DOME PROPERTIES
Volumetric
Spherical structures enclose
the greatest volume
with the least surface
of any type of structure.
Every time the diameter
of a spherical structure
is doubled
surface area increases 4 times
and
volume increases 8 times.
Dome volume increases
at a 3rd power rate,
while
the structural component lengths increase
at only a fraction more than an arithmetical rate.
The weight gain of the structures
as ratioed to basic linear dimensions[diameters],
is as 1 is to 1-(1/x) weight ratio,
as the same structure
is multiplied in relative size.
Every time the linear dimension
of a symmetrical structure is doubled,
the surface area of the enclosure increases
at a 2 to the 2nd power rate and
its volume increases
at a 2 to the 3rd power rate.
Aerodynamic Thermodynamic
Wind drag on a dome,
as quantified in the Drag Coefficient.
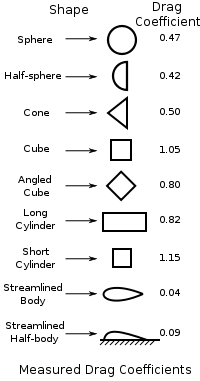It is less for a Spherical structure
than for Rectilinear Structutures
but not as low as for Streamlined Shapes.
Bernoulli Chilling Effect
As the suns radiation
is outwardly and diffusingly reflected
by the domes convex outer surface,
vertical thermal-column movements
of the sun heated outside atmosphere
develop.
The spirally rising volumes of heated atmosphere
will draw air out from under
the domes large lower edge summertime openings.
This voluminous outward drafting
in turn pulls air into the dome
through the small cross sectioned ventilators
at the domes apex.
The pressure differential
between the small air entry
and the large exhaust openings
produces the BERNOULLI CHILLING EFFECT,
which in hot weather will swiftly cool
the domes interior atmosphere.
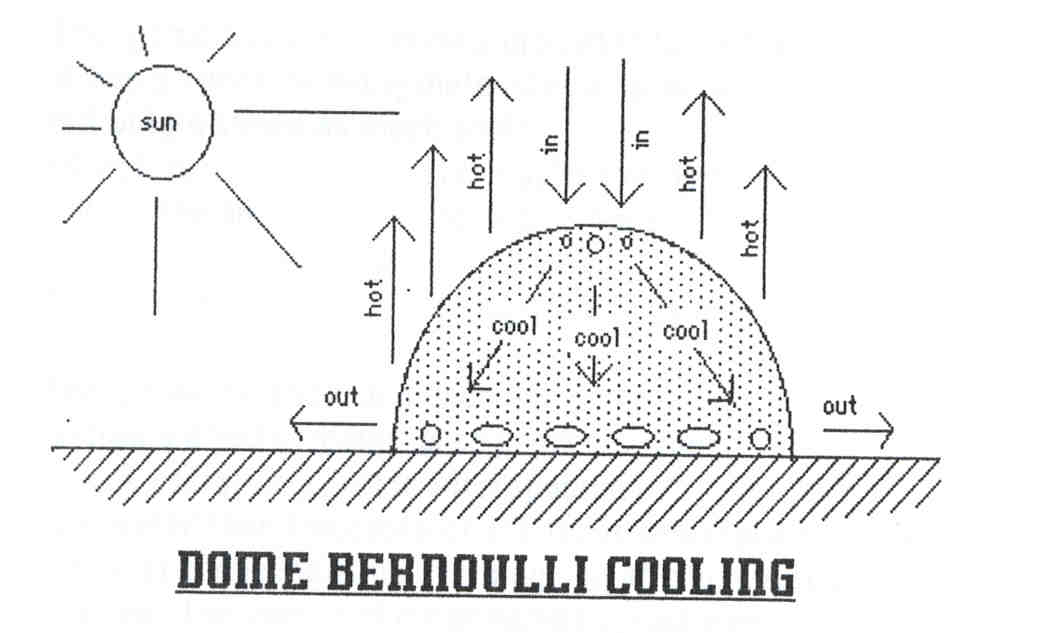Upward draft is caused
by polar heating of the outside surface
which then heats the surrounding air.
The warm air rises
creating a thermal column.
Air is sucked out
of the large openings
at ground level
causing reduced pressure
inside the dome.
Reduced pressure causes
air near the top vent
to rush in
through the small openings.
Increased air flow
through these small openings
cools incoming air.
This aspect of dome behavior
maybe one of the hardest to replicate.
As of 12-16-2013,
I have not been able to achieve
Bernoilli cooling.
Perhaps it is a matter
of adequate insulation and reflectivity
in dome construction
and scale maybe a factor.
Most of my large domes,
have had tranlucent skins
which tend to get extremely hot
when exposed to the sun
without shades.
I have tried some
small model size domes
of various sizes
out of highly reflective metal
and attempted to measure
a temperature difference
due to Bernoulli Cooling
with no luck as yet.
Heat Sinking
Heat energy
is more efficiently retained
in large spherical structures
than by smaller domes.
When the spherical structures diameter doubles,
the ratio
of the amount of enclosing surface
through which an interior molecule of atmosphere
can gain or lose energy as heat or cold
to the Volume of the interior
is halved.
Everytime
a geodesic domes diameter
is doubled,
it has 8 times
as many molecules of atmosphere
but only 4 times
as much shell;
therefore
each progressive doubling
of dome diameters
halves the amount of enclosing surface
through which a molecule
may lose or gain heat energy
relative to the enclosed volume.
Every time we enclose a geodesic dome
within a greater diametered geodesic dome,
whose radial concentric inter-spacing
is greater than the Frost Depth
where the dome is located
while at the same time
avoiding use of any metal connections
between the inner and outer domes structures,
the heat losses and gains
of the innermost dome
is halved
with respect
to those of non-domed-over-domes
of the same dimensions.
Frost Line Depth Map
In summary,
a very large
unconnected dome-within-a-dome
offers best insulation from the outside environment.
BUT.....
What happens when you nest 3 or more domes ?
How does that math work ?
...and at what size of structure
do you start to realize a useful effect ?
For instance,
what happens inside
when you have a nested 40' radius and a 32' radius dome
compaired to an un-nested 32' dome ?
Stay tuned.....
Next
Table of Contents