SOLID GEOMETRY


SOLID GEOMETRY

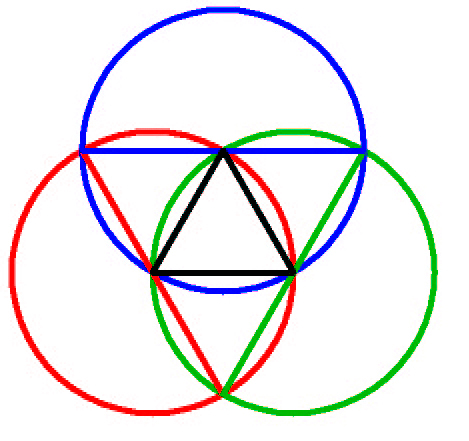
Webster defines  Geometry 
as " a branch of mathematics 
concerned with
the properties, measurements and relationships 
of points, lines, angles, surfaces, and solids ".

Much of geometry 
was described 
by the ancient Greek mathematician Euclid.

 Euclidean Geometry  
is based upon axioms.

An Axiom 
is a postulate 
advanced as an essential premise 
of a train of reason.

The following are Euclidean axioms:

A point 
is a geometric element 
(a place in space)
being determined 
by a single ordered set of coordinates.

A line 
is a geometric element 
that is generated 
by a moving point 
and has extension 
only along the path of the point. 

A straight line
is generated by a point 
moving continuously 
in the same direction 
and is expressed 
by a linear equation .

A locus 
is the set of all points 
determined 
by stated conditions.

A plane 
is locus of such nature 
that a straight line 
joining any 2 of its points
lies wholly in said locus.

A polygon 
is a closed planar figure 
bound by straight lines 
or great circle arcs.

These Axioms 
provide us with definitions 
and a basis for discussion.

Fuller's approach to geometry 
was experimental,  thus scientific. 

He looked to nature
and asked what are basic natural laws
associated with geometry and structure.

One of Fuller's early mathematical discoveries 
was the fact that triangles - 
regular, isosceles and scalene- 
may be modularly subdivided 
to express second-powering.


Triangles are the basic polygons - 
i.e. all polygons are reducible to triangles  
and are further irreducible. 

The fundamental principle 
of finite local system mathematics
is that the the universe 
is divided 
into 2 main parts, 
the withinness and the withoutness.

The triangle is the simplest divisor 
of space into withiness and withoutness
using straight lines.

Any triangle 
whose 3 edges 
are each evenly divided 
into the same number of intervals, 
and whose edge-interval marks 
are cross-connected with lines 
that are inherently parallel 
to the triangle's respective 3 outer edges -
will be subdivided by little triangles 
all exactly similar 
to the big triangle thus subdivided,
and the number of small similar triangles 
subdividing the large master triangle 
will always be the Second Power 
of the number of edge modules of the big triangle. 



In other words,
we can say "triangling" 
instead of "squaring"
and since all squares 
are subdividable into 2 triangles 
and since each of these triangles 
can demonstrate a real second-powering, 
and since nature 
is always most economical 
and since nature 
requires structural integrity 
of her forms of reference,
she must be using "triangling" 
instead of "squaring" 
when any integer
is multiplied by itself.


Another non-Ionian Greek, 
Pythagoras, 
demonstrated and "proved" 
that the number of square areas 
of the unit-module-edged squares 
and the number of cubical module volumes 
of the module-edged-cubes
correspond exactly 
with arithmetic's
second-powerings and third-powerings. 

The Greeks 
and all mathematicians and scientists, 
have ever since assumed 
these square and cube results 
are the only possible products 
of such successive inter-multiplying 
of geometry's unit-edge-length modular components.  


SOLIDS


Solids 
are geometrical elements 
having 3 dimensions.

Polyhedra 
are solids 
formed by planar faces (polygons).

There are three intrinsically stable regular polyhedra:                               
the tetrahedron (4 sided), 
the octahedron (8 sided polyhedron),               
and the icosahedron (20 sided).

These three polyhedra 
all have equilateral triangular sides
and are the solids 
from which geodesic domes are derived
(primarily the icosahedron).

NATURAL ORDER OF GEOMETRIC FIGURES 
There is a Natural Order of Geometric Figures 
that results from the intersection of Unitary Lines.
Unitary Lines are lines being 1 unit in length.
If we progress from 1 onward in increments of 1 
for the number of lines impenging on a point
and if we connect each of these lines other ends 
with unitary lines
we find that a Natural Order of Geometric Figures result.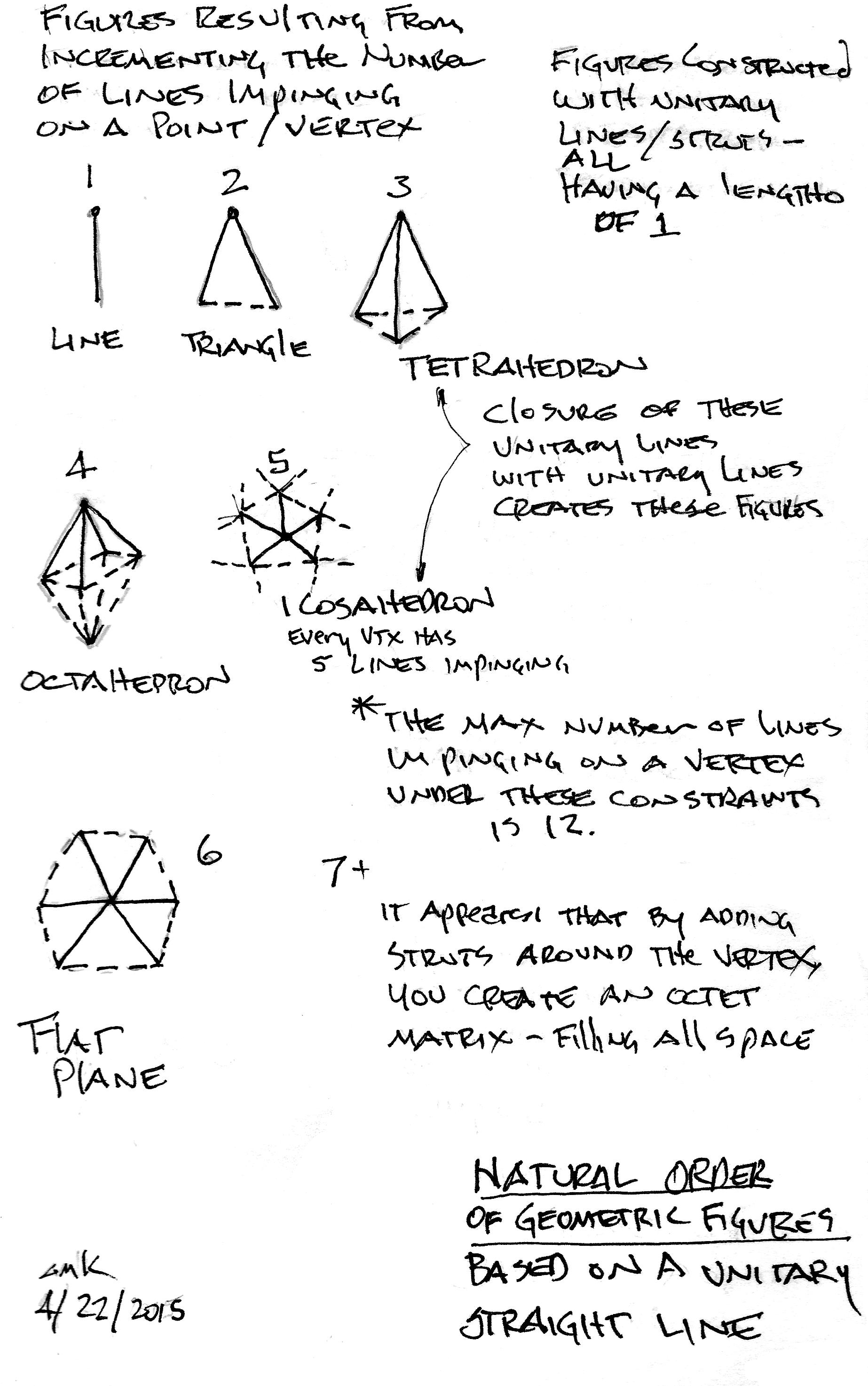


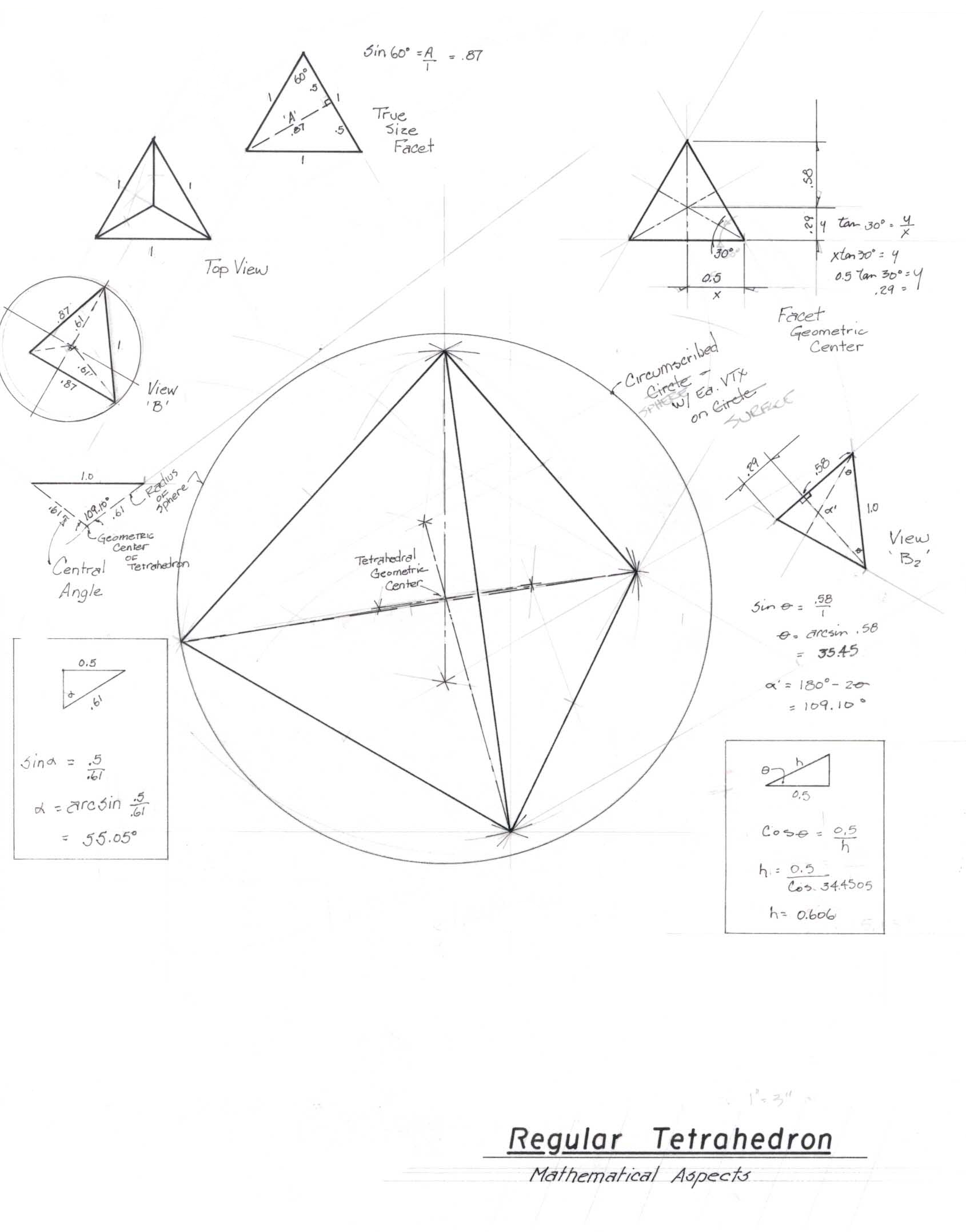
THE TETRAHEDRON 

The Tetrahedron 
is the basic structural system.

All other structure 
is a transformative phase or complex 
of tetrahedronal transformations.

The tetrahedron (4 faceted structure) 
is the minimum-prime divisor
of omnidirectional universe 
into 2 fundamental domains - 
the withinness & withoutness, 
the included & excluded, 
the microcosm & macrocosm.

All polyhedra maybe subdivided 
into component tetrahedra; 
no tetrahedron 
maybe subdivided 
into component polyhedra 
of less than 4 faces.

The regular 6 chord edge tetrahedron encloses (defines) 
the minimum volume with the most surface area 
of all geometric polyhedra (structural systems).

Of the three prime structural systems of universe, 
the tetrahedron is the strongest
per unit volume enclosed.

When stressed with a high relative internal pressure, 
all polyhedra tend to define 
the maximum volume with minimum surface;
toward the spherical convex-arc edged tetrahedra.

When stressed with a high relative external pressure, 
structures tend to enclose 
minimum volume with maximum surface - 
the chordal or concave tetrahedron
being the 4 webbed interaction 
between the 6 exterior edges of the tetrahedron 
& its center of gravity).

The regular tetrahedron is the zero phase
between the convex tetrahedron & concave tetrahedron.

Chordal-edged tetrahedronal structures best resist external forces
& their vertices best resist concentrated loads.

Arc-edged tetrahedra best resist internal pressures 
& their surface arc vertices best resist 
concentrated internal pressure & impact forces.

Both chordal edged tetrahedra & arc-edged tetrahedra 
permit omnidirectionally valved penetrations.

Any non-equi-edged quadrangle 
with each of its 4 edges uniformly subdivided 
into the same number of intervals 
and with those interval marks interconnected, 
produces a pattern of dissimilar quadrangles. 

In the same manner,
all tetrahedra, octahedra, cubes 
and rhombic dodecahedra-regular or skew-
can be unitarily subdivided into tetrahedra 
with the cube consisting of 3 tetra, 
the octahedron of 4 tetra, 
and the rhombic dodecahedron of 6 similar tetra; 
and that when any of these regular or skew polyhedras' 
similar or dissimilar edges and faces 
are uniformly subdivided and interconnected, 
their volumes would always be uniformly subdivided 
into regular or skew tetrahedra, 
and that N^3 can and should be written N^tetrahedroned 
and not as N^squared.

Nature would use the tetrahedron as the module of subdivision
because nature has proven,
to the physicists and the other physical scientists,
that she always chooses the most economic realization. 

Cubes require 3 times as much Universe as do tetrahedra 
to demonstrate volumetric content of systems 
because cubic identification with third-powering 
used up three times as much volume as is available in Universe. 
As a result of cubic mensuration 
science has had to invent 
such devices as "probability" and "imaginary numbers". 
Thus "squaring" and "cubing" 
instead of nature's "triangling" and "tetrahedroning", 
account for science's using mathematical tools 
that have no physical-model demonstrability- 
ergo, are inherently "unscientific".

If the Greeks had tried to do so, 
they would soon have discovered 
that they could not join tetrahedra face-to-face to fill all-space; 
whereas they could join cubes face-to-face to fill all-space. 
Like all humans they were innately intent 
upon finding the "Building-Block" of Universe. 

The cube seemed 
to the Greeks, the Mesopotamians, and the Egyptians 
to be just what they needed 
to account their experiences volumetrically. 

But if they had tried to do so, 
they would have found that unit-dimensioned tetrahedra  
could be joined corner-to-corner 
only within the most compact omnidirectional confine 
permitted by the corner-to-corner rule,
which would have disclosed 
the constant interspace form of the octahedron 
which complements the tetrahedron to fill all-space; 
had they done so, 
the Ionians would have anticipated 
the physicists' 1922 discovery  of "Fundamental Complementarity" 
as well as the 1956 Nobel-winning physics discovery 
that the complementarity 
does not consist 
of the mirror image of that which it complements. 

But the Greeks did not do so, 
and they tied up humanity's accounting with the cube 
which now, 
2,000 years later, 
has humanity in a lethal bind of 99% scientific illiteracy.

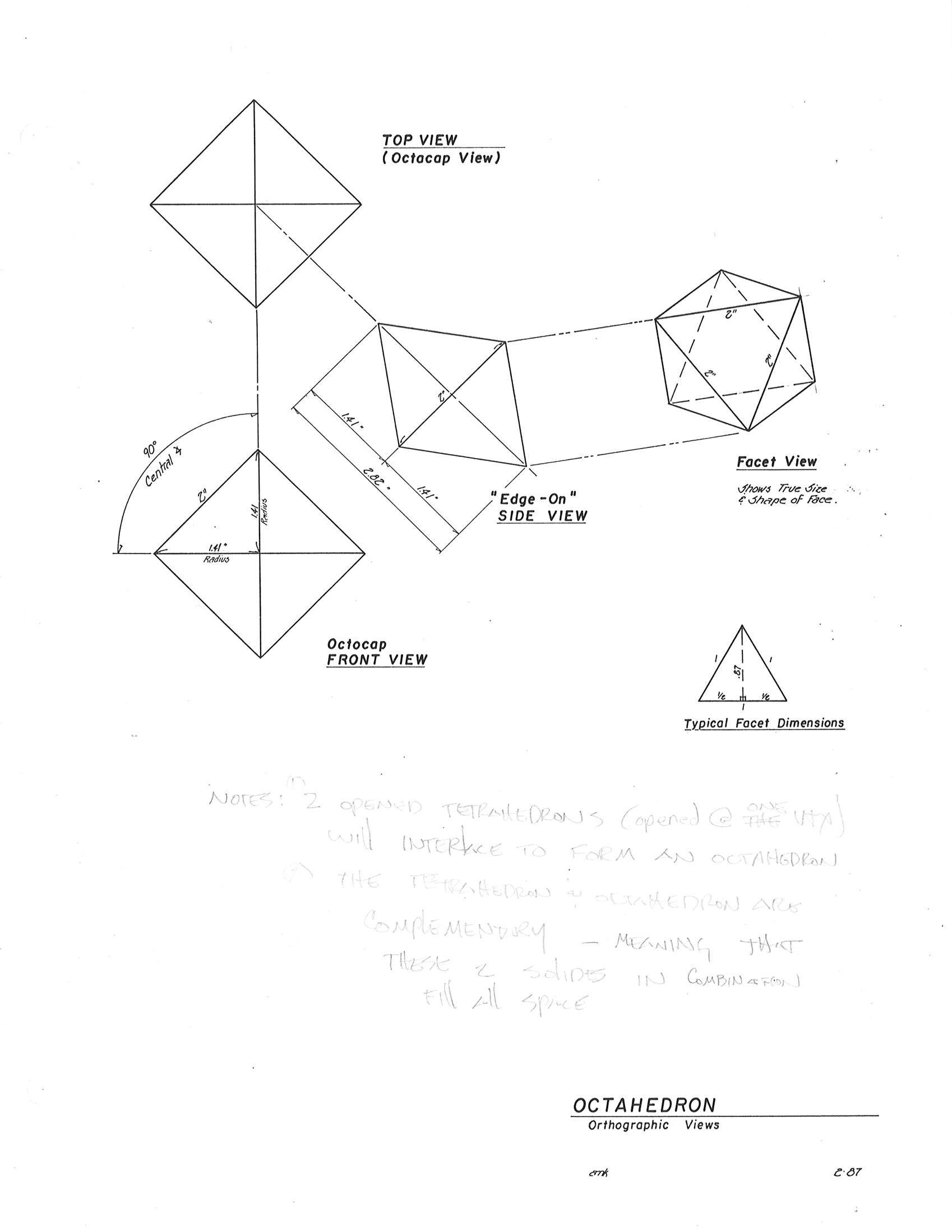
The OCTAHEDRON

The regular octahedron 
is an 8 sided 
triangular faceted polyhedra.

The Octahedron 
is the complement 
of the Tetrahedron
to fill all space. 

It automatically is formed 
when Tetrahedrons are joined 
corner to corner
on a plane.

The octahedron 
is the prefered system 
for a balance 
of strength and volume.

An octahedron 
consists of 
12 vector edges 
and 2 units of quantum 
and
has a volume of 4 
when the tetrahedron 
is taken as unity.

The octahedron 
represents 
the most commonly occurring 
crystallographic conformation 
in nature. 

It is the most typical 
association of energy as matter, 
it is at the heart of such association. 

Any focus 
in the gravitational pull 
of the rest of the universe 
upon the octahedrons symmetry
precesses it 
into asymmetrical deformation 
in a plane at 90 degrees
to the axis of exaggerated pulling.

This forces one of the 12 edge vectors of the octahedron 
to rotate at 90 degrees. 

If we think 
of the octahedron's 
3 XYZ axes and its 6 vertexes, 
oriented in such a manner
that X is the north pole an X' is the south pole, 
the other 4 vertexes - Y,Z,Y', Z'- 
all occur in the plane of, and define, the octahedrons equator. 

The effect of gravitational pull upon the octahedron 
will make one of the 4 equatorial vectors 
disengage from its 2 adjacent equatorial vertices, 
thereafter to rotate 90 degrees 
and then rejoin its 2 ends with the north and south pole vertices.
When this precessional transformation is complete, 
we have the same topological inventories 
of 6 vertexes, 8 exterior triangle faces, and 12 vector edges 
as we had before in the symmetrical octahedron, 
but in the process 
the symmetrical, 4-tetrahedra-quanta-volumn octahedron
has been transformed into 3 tetrahedra (3-quanta volume)
arranged in an arc section of an electromagnetic wave conformation
with each of the 2 end tetrahedra 
being faced bonded to the center tetrahedron.

THE ICOSAHEDRON

An icosahedron 
is a polyhedron 
of 20 faces.

A spherical icosahedron 
is an icosahedron 
'exploded' 
onto the surface of a sphere ; 
it bears the same relation to an icosahedron 
as a spherical triangle to a plane triangle - 
the edges 
of the faces of the spherical icosahedron 
are all geodesic lines.

The icosahedron 
is the least strong 
prime structural system
but encloses 
the greatest volume 
per unit of invested energy.

See the appendix for models of the 3 basic solids.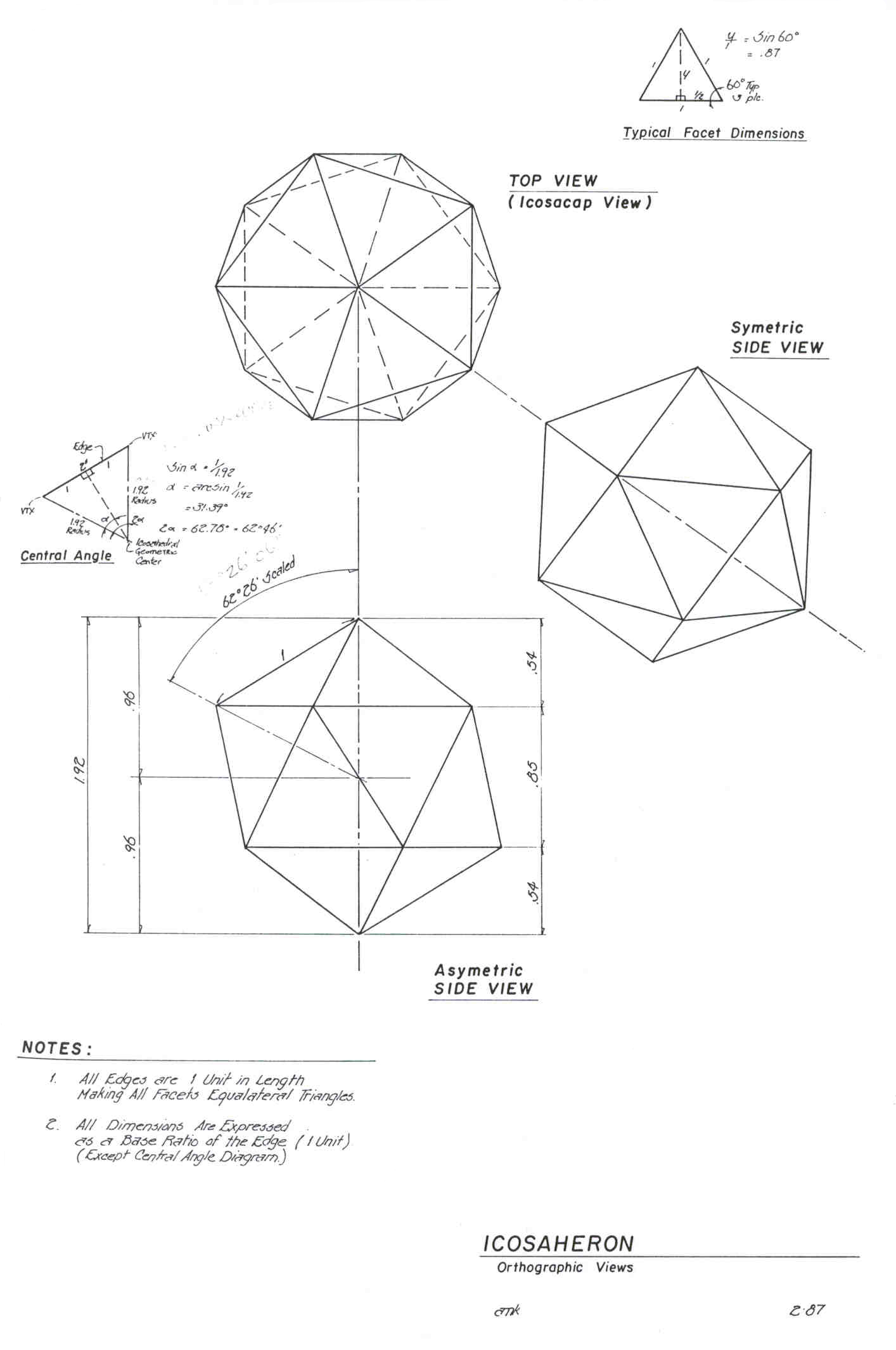

POLYHEDRAL MULTIPLICATION

The Euclidean Greeks 
assumed not only 
that the millions of points and instant planes 
existed independently of one another, 
but that the complex 
was always 
the product 
of endless multipliable simplexes 
- to be furnished 
by an infinite resource 
of additional components. 

The persistence 
of the Greek's original misconceptioning 
of geometry 
has also distorted 
the conditioning of the human brain-reflexing 
as to render it a complete 20th century surprise 
that we have a finite universe: 
a finite 
but non-unitarily and non-simultaniously accomplished, 
eternally regenerative Scenario Universe. 

In respect 
to such a Scenario Universe multiplication 
is always accomplished only by progressively complex, 
but always rational, 
subdividing 
of the initially simplest structural system of Universe: 
the sizeless, timeless, generalized tetrahedron. 

Universe, 
being finite, 
with energy 
being neither created or lost 
but only being nonsimultaniously intertransformed, 
cannot itself be multiplied.

Multiplication 
is 
cosmically accommodated 
only by further subdividing.


Next
Table of Contents